Zeng Nanjin, Huang Yebin, Li Shuqi, Liu Yixin, Zhang Yichen
programme:Master of Economics (quantitative economics) in National University of Singapore
Our research group members have a review about Nelson and Siegel’s famous paper, Parsimonious Modeling of Yield Curves. This review contains 3 sections. Section 1 summarizes the paper. Section 2 demonstrates how to use Nelson-Siegel model to fit the yield curve, with data of Chinese government bonds. Section 3 is our comment.
1.Summary
Inspired by expectation theory of term structure of interest rates, this paper introduces a parametrically parsimonious model for yield curves. The model aims at providing a more concise method to capture potential relationship between yields and maturity and to describe different shapes of yield curves: monotonic, humped and S shaped. In the empirical part, the authors select 37 samples, to test the ability of the second-order model of describing the relation between term to maturity and yield for U.S. Treasury bills. These samples come from Federal Reserve Bank of New York quote sampled sheets, from January 22nd 1981 to October 27th 1983. By calculating bill prices using discount yields, the authors then calculate the continuously compounded rate of return from delivery date to maturity date. The rate of return would be annualized to a 365.25-day year. The parameterized model is following:
\[R(m)=a+b*\frac{[1-exp(-\frac{m}{\tau})]}{\frac{m}{\tau}}-c*exp(-\frac{m}{\tau})\]
Firstly, the authors compute two regressors’ sample values for any provisional value of τ, and then use linear least squares method to find the optimal-fitting value of coefficients a, b and c. The result shows that the model explains part of the variation in yields: almost 0.96.For τ = 50, the overall precision of fit is high, but the precision of fit for each data sets is not high enough. Furthermore, the authors plot the three parameters of the forward rate function: short-term, medium-term, and long-term, to observe the evolution of second order model over time. In part III, the authors study maturity and issue effects by analyzing residuals. They find that issue effects differ from maturity effects because they are related to bills maturing at specific dates rather than to bills with specific terms to maturity. Finally, the authors forecast long-term bond prices to test whether this model is satisfactory. The result shows that the correlation between actual prices and predicted prices is 0.96, a relatively high value. However, long-term discount rates will be overestimated by the model if yields are generally high and the yield curve has a downward trend. In this case, bond prices will be underestimated.
2.Method Demonstration
2.1 Data and model setting
We collect the maturity period and the corresponding yield rate data of Chinese bonds from China Central Depository & Clearing Co., Ltd. (CCDC). There are 15 maturity periods in our sample: 0.08, 0.17, 0.25, 0.5, 0.75, 1, 3, 5, 7, 10, 15, 20, 30, 40, and 50 (years). Besides, we set the sample period from January, 2017 to November, 2019, including every last Thursday in 36 months. The parsimonious Nelson-Siegel (NS) model we used to fit the yield curve is:
\[R(m)=\beta_{0}+(\beta_{1}+\beta_{2})*\frac{[1-exp(-\frac{m}{\tau})]}{\frac{m}{\tau}}-\beta_{2}*exp(-\frac{m}{\tau})\]
2.2 Empirical Result
As the paper did, we firstly fit the yield curves for every single month, which produces different parameters for one-month data. The statistical result of the four parameters is shown in the table 1 below. Since each cross section corresponds to one different τ in the parsimonious NS model, the parameter is not stable and changes with time. As can be seen from the table, the standard deviation of parameter estimates is large.
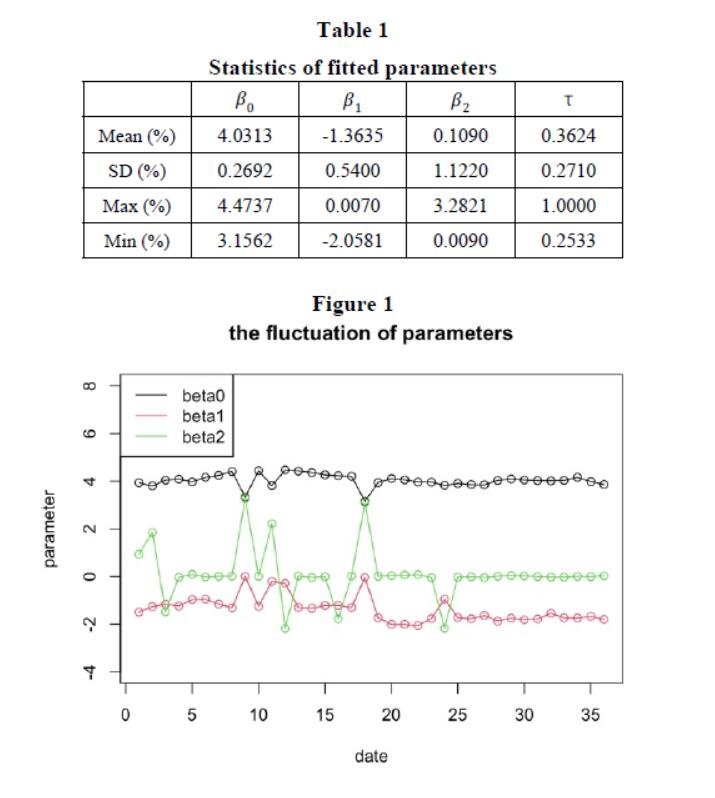
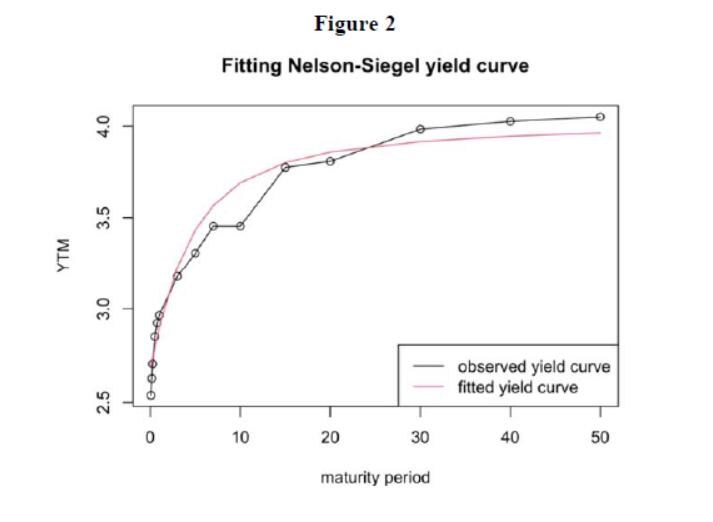
Then we report the fitted yield curve using the average of parameters. As can be seen from the observed yield curve in Figure 2, YTM increases as the maturity period increases. The model fitting effect obtained by us is generally good.
3.Comment
As we discussed in Summary part, this paper constructs a parametrically parsimonious model, the Nelson-Siegel model, with a class of functions, to capture three kinds of yield curves successfully. Firstly, the model avoids a common weakness of previous polynomial models which behave poorly in long term. Moreover, the components of the model could be interpreted as short term, medium term and long term, which makes the model easier for users to comprehend. As we looked up related literatures, we found the Nelson-Siegel model (and its adapted versions) are still widely used by scholars, investors and policy makers for fitting the yield curve of government issued bonds, which could be the evidence for the model’s contribution to industry and research. Furthermore, in the view of literature writing, this paper is worth studying. The paper starts at expectation theory and literature review, uses rigorous mathematical argument to derive proper functions for the model, gives real data sample to demonstrate the method and holds a comprehensive discussion about the results. Throughout the paper, the authors’ logic is clear and credible. Though the paper is nearly perfect, we group members have some ideas that deserve further discussions.
- In the empirical part, one noticeable point is that, for each set of data, the method requires to find an optimal value of τ, which varies among data sets. However, the authors state later in the paper, to choose a unique τ for all data sets only makes a little loss in fitting accuracy. Another noticeable point is that the forward rate components β1, β2, β3 is unrelated scatter points among time horizons. These two points make it difficult to study the trends of these components and to interpret them in the view of economics. With these doubts we looked up literatures and found one of its improved versions, the Dynamic Nelson-Siegal model. The dynamic model uses a unique τ for all data sets and defines β1, β2, β3 as three time-series sequences, which makes the prediction and trend study in forward rate components become available. For instance, some economists analyze the relationship between macro-factors and these components in order to predict term structure in the future.
- In the regression for U.S. Treasury bills, the authors use maturities from 3 to 178 days. We group members are curious about the reason why the authors constraint the maturities in their data set among such a short period. If the authors add other longer maturities into the regression, for example, bonds which mature in 10 years and 30 years, the problem of prediction out of sample may not exist. Adding longer maturities may improve the accuracy and reliability of the prediction. To conclude, we group members consider that the paper is extraordinary both in theory quality and in literature writing. The Nelson-Siegel model is one of the most important models in yield curve analysis, with remarkable contribution to industry and research. Our empirical try of fitting yield curves for Chinese government bonds also shows that the Nelson-Siegel model could give generally reliable results.
Bibliography
Guo, Jimin, and Jiawei Zhang. (2016). Based on Nelson-Siegel Model to Predict the Chinese Government Bond Yield Curve. China Bond, 49: 66-72.
Nelson, Charles R., and Andrew F. Siegel. (1987). Parsimonious Modeling of Yield Curves. The Journal of Business, 60(4): 437-489.
