Zeng Nanjin, Huang Yebin, Li Shuqi, Liu Yixin, Zhang Yichen
programme:Master of Economics (quantitative economics) in National University of Singapore
Our research group members go further to review the origin of this amazing theory, the famous paper, Portfolio Selection. Our work includes 3 sections. Section 1 is a summary of this paper. Section 2 is a empirical data application. Section 3 is our comment.
1.Summary
The main idea of Markowitz’s Portfolio Selection is to put forward a quantifiable method to balance the expected return and the risk of different portfolios, and to proof that this method can get a set of effective portfolio. The method determines a set of efficient combination to minimize variances of returns(V) under the condition of a given the expected return (E), or to maximize E under the condition of a given V. Using E-V method, proportions of each securities in the effective portfolio can be obtained; furthermore, the set of effective portfolio can be obtained. investors can choose the portfolio from the set and make their investment decisions according to their own risk preference.
In particular, the paper mainly discusses the selection of definite portfolio, if belief of future performances are given. This paper rejects the traditional investment rulesthat investors should invest all funds in the security that has the maximum discounted or expected value of return or only diversifies investment among securities with maximum return. After points out deficiencies of the investment rules above, Markowitz proposes a new selection rule–“expected returns-variance of returns” rule (E-V rule) and gives proof by geometric means.
Taking the proportion of various securities in the portfolio as a variable, the portfolio problem of finding the minimum risk with a fixed return is simplified to a quadratic programming problem under linear constraints. After he worked out the shapes of isovariance curves and isomean for n-security case, he specifically described the process to get the shape of the attainable set in the 3-4 security cases. When point falls inside the attainable set, that selection of portfolio is efficient. The point has the minimum V with a fixed E or the maximum E with a given V. During the elaboration of the method, this paper points out that good portfolios are not simple combinations of excellent individual securities and diversification is better than single asset investment generally, an investor should take the correlation of different securities into account. The author also proposes that diversifying securities in different industries is a good way to lower high covariances among securities. In the end, this paper briefly describes the application of theoretical analysis and practice investment selection.
2.empirical data application
2.1 Data and model setting
We collect all 300 individual stocks of CSI 300 Index from Wind database to be our sample securities which are good representations of the stock market due to their high liquidity and active-trading performance. We set the sample period from January 3 to August 20, 2020, including 153 trading days. Furthermore, Return can be calculated as:
\(R_{it}=\frac{P_{i,t}-P_{i,t-1}}{P_{i,t}}\).
where \(R_{it}\) denotes the daily return of stock i on date t.
\[r_{i}=E(R_{it})\] \[\sigma_{i}^{2}=Var(R_{it})\] \[\sigma_{ij}=E\{[R_{it}-E(R_{it})][R_{jt}-E(R_{jt})]\]
where \(r_{i}\) , \(\sigma_{i}^{2}\) represent the expected value and the variance of daily return separately, and \(\sigma_{ij}\) denotes the covariance between \(R_{i}\) and \(R_{j}\).
Thus, according to Markowitz Mean-Variance Model(Markowitz, 1952),for one combined portfolio with N securities, the expected return (E) and the variance (V) is:
\[E=\mathop{\sum_{i=1}^{N}X_{i}r_{i}}\] \[V=\sum_{i=1}^{N}\sum_{j=1}^{N}\sigma_{ij}X_{i}X_{j}\]
where \(X_{i}\) is the percentage allocated to the i security, \(X_{i}>=0\) , \(i=1,2\ldots N\). By associating E and V, we can obtain efficient portfolios to construct the efficient frontier.
2.2 Empirical Result
We established two groups of which one is from the same industry (bank group) and the other is diversified among varied industries (diversified group). Then we compare efficiency of diversification in two ways: the first is to compare the two groups by given the same number (5 or 25) of securities. The second is to compare different sample size of groups. All securities of these groups are randomly selected from 300 individual stocks of CSI 300 Index.
The table 1 shows the minimum of correlation coefficients in different groups. It is obvious that securities from the same industry have a much higher correlation.
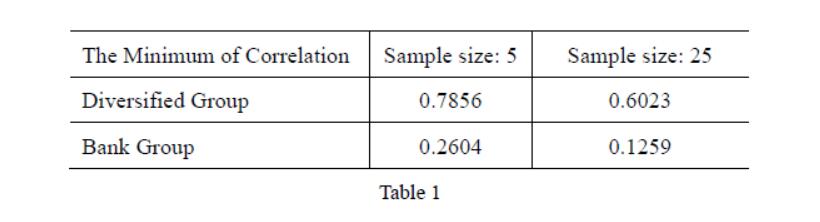
With the aid of R program software, we construct the efficient frontiers of groups which directly shows the difference between them.
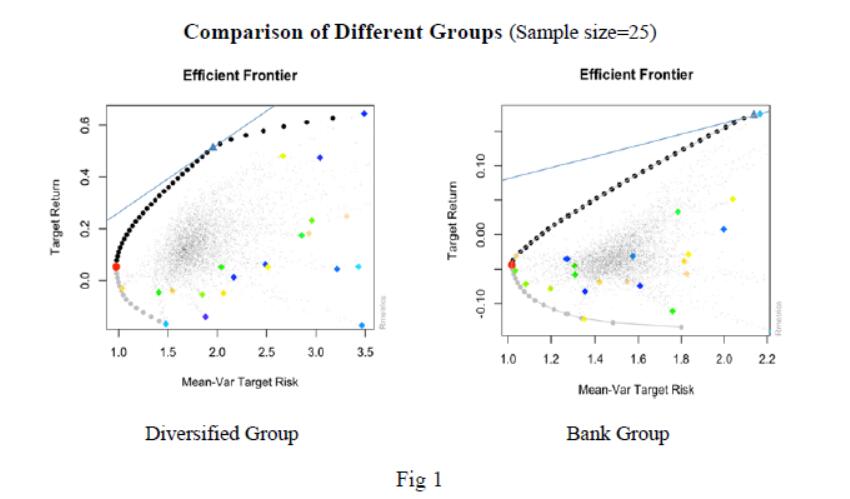
According to Fig 1, nearly all single stocks (colored diamond squares) are in the right of the efficient frontiers (the curve of the black dots), illustrating that diversification of securities can decrease variance for given E. Besides, investing stocks among different industries can also decrease risk since given the same targeted return, the diversified group has lower variance. Furthermore, as shown in Fig 2, increasing the size of portfolios can lower the risk of investors.
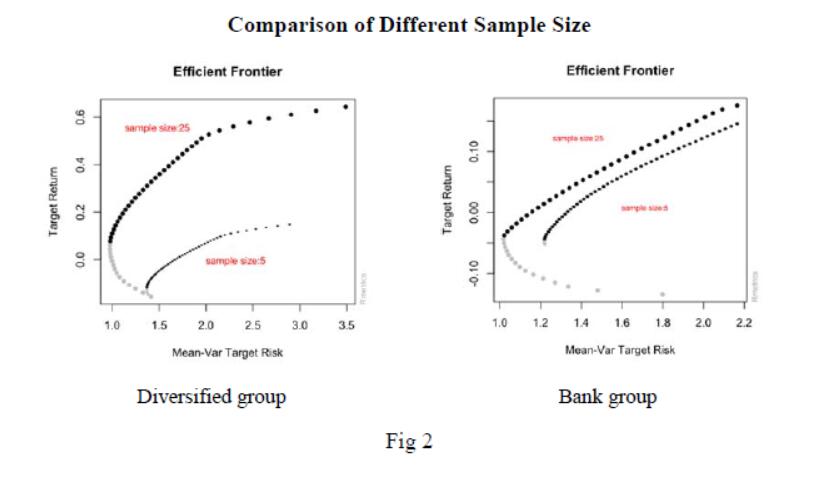
In conclusion, diversification of risk among different industries or more numbers of securities can lead to a better-performed portfolio strategy.
3.Conclusion
After discussion, our group members have some common thoughts to this paper. Above all, as we mentioned in section 1, this paper makes large contribution to the finance industry. Firstly, this paper is the first paper which put forward a practical and quantifiable method to link the most two important idea, return and risk. Therefore, investors can make their best decisions according to their own risk preference. Another important change this paper brought to the industry is that, the paper separates bankers into two specialized groups, analysts and consultants. Analysts concentrate on finding the effective portfolio using quantitative methods, while consultants concentrate on giving investment advices based on each customer’s preference. This means that more individual investors could participate the market through professional agents, which enlarge the financial markets.
However, at the view of people from 68 years later, this paper has some limitations which could be further improved with advanced mathematical and programmatic tools.
-
For the paper, it lacks of comprehensive evidence for the viability of this new R-V method. As the author states in page 79, he only gives the examples finding the attainable set in the 3 and 4 security cases. On the contrary, these days, the number of listed companies has increased into a huge number. For example, there are 1750 listed company in Shanghai stock exchange. The author could not guarantee that the R-V method could apply to the case of this large number of securities, without a rigorous mathematical proof for N securities. Another probably improvement is that, we could use programming software and empirical data to test the viability of this new R-V method. In the 1960s, it was very difficult to compute the covariance matrix and handle the historical data, which made the analysis with large number of securities seemed to be impossible. However, with R program, we could perform this kind of analysis effectively, as our group members showed in section 2.
-
For the theory, its validity depends much on the “expected return” and the “expected variance”. Though the author states that it should be determined using statistical techniques and human judgement, some problem could occur in the practical use. Consider the case when a listed company performs assets reorganization. For instance, we have constructed a portfolio with 5 oil companies. Now, one company of them declare that it would purchase asset and turn into a textile company. On the one hand, historical data would not show the effect on covariance instantly, since it takes time to generate new data under new conditions. On the other hand, we could not depend on human judgement completely, otherwise we go back to old way doing speculation instead of investment. The result is that it is difficult for me to make reasonable decision using the EV method, until enough historical data is generated. A probably way to evaluate the effect of these market events is also to use empirical data to test the theory. We could simulate different strategy, such as taking out this kind of stock, or just neglecting them. And then we could compare the result of these different strategy and give prediction how these events affect the validity of E-V method. In short, using simulation, we could give much convincing evidence about the validity of portfolio selection.
Though the paper has some limitations, our group members regard it as one of the most important papers in finance industry. The author used relatively comprehensible and intuitive way to illustrate E-V method and effective portfolio clearly.
references
Li, Shanmin, and Pei Xu. 2000. “Research on the Application of Markowitz’s Portfolio Theory Model.” Economic Science, 82(1): 42-51.
Markowitz, Harry. 1952. “Portfolio Selection.” The Journal of Finance, 7(1): 77-91.
Zhang, Heqing. 2015. “Research on Markowitz Theory Model of Mean and Variance Changing.” Dissertation for the Master Degree in Economics, Harbin Institute of Technology. https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD201601&filename=1015981115.nh
