Nanjin Zeng(id:15220162202482) WISE IUEC 2016
You can also get a .lyn version in the same github folder because it is written with latex.
1.Introduction
In the lecture, we have learnt the new idea of an amazing method, Regularization.
In the Econometric course which I attended in last semester, I know about the OLS method. It is an Best Linear Unbiased Estimator. It seems nothing better than OLS because the economists concerns about causal relationship without bias. But for this case, I know the new idea that we could sacrifice the unbias and achieve low variance, which could improve the accuracy by reducing the out-of-sample error significantly. That is why I want to learn more about how this idea formed and been improved.
In this blog, I would carry out a brief look about how the regularization developed from Ridge to Lasso. A method the Nonnegative Garrote (Breiman, 1993) would be talked because it is a method invented before the Lasso, which offsets some drawbacks in the Ridge and has some similarity with Lasso. It is indispensable as the motivation for the lasso.[1] I would introduce them one by one in a contribution view, what improvement they had made comparing to the previous one.
2.The Development path
2.1 the Ridge
The Ridge regression is a biased estimation invented by Hoerl and Kennard (1970). Its feature has been showed in the lecture. But in the papar, the authors give us a different view of the Ridge using the matrix, which could help us understanding the mechanism of Ridge.
In the standard model of mutiple linear regression, the parameter is estimated by
\(\hat{\beta}_{OLS}=(X'X)^{-1}X'Y\).
This estimation procedure is a good one if \(X'X\), when in the form of a correlation matrix, is nearly a unit matrix.[2]
To be brief, it means that the condition for OLS to work well is that \(X'X\) does not equal to 0. It requires the \(X\) is a non-singular matrix. But there is some case in which \(X'X\) is close to zero, in which case the variance is huge for \(var(\hat{\beta}_{OLS})=\sigma^{2}(X'X)^{-1}\), when[3]
-
There is too many predictors. (p>N)
-
There are strong correration between some predictiors. (Multicollinearity)
These two problems rarely occurs in our previous study. When we begin to learn ecometrics, we choose a small number of predictors stepwisely using the old criteria if the coefficant is statistically significant. But for big data science, we face a large number of predictors each have different levels of effect on the dependent variable. Doing stepwise subset selection is time-costly and has some other problems.
One of the solution is doing the Ridge regression. In this way, the parameter is estimated by[4]
\[\hat{\beta}_{R}=(X'X+kI)^{-1}X'Y=WX'Y\]
It could ease the problem 2 by create an invertible matrix. Furthermore, it could avoid probably overfit by reducing the variance of estimators.
2.2 the Nonnegative Garrote
But the Ridge still have some drawbacks,[5]
-
The Ridge gives a regression no simpler than the OLS.
-
The Ridge is not scale invariant. If the scales used to express the individual predictor varibles are changed, then the ridge coefficients do not change inversely proportional to the changes in the variable scales.
For drawback 1, it needs something like subset selection which could determine a smaller subset that exhibits the strongest effects. For drawback 2, the new method should be scale invariant. That comes the Nonnegative Garrote.
The procedure of the Nonnegative Garrote is[5]
Let \(\{\hat{\beta}_{OLS}\}\) be the original OLS estimates
Take \(\{c_{k}\}\) to minimize \(\sum_{k}(y_{n}-\sum_{k}c_{k}\hat{\beta}_{OLS}X_{kn})^{2}\) under the constraints \(c_{k}\geq0, \sum_{k}c_{k}\leq s\)
Then \(\hat{\beta}_{NNG}=c_{k}\hat{\beta}_{OLS}\)
As the Garrote is drawn tighter by decreasing s, more of the \(\{c_{k}\}\)becomes zero and the remaining \(\hat{\beta}_{NNG}\)is shrunken.
By this way, the Garrote eliminates some variables which do not have large effect on dependent variable. To be intuitive, let us compare the form of the nn-garrote coffients \(\hat{\beta}_{NNG}=(1-\frac{\lambda^{2}}{\hat{\beta}_{OLS}^{2}})^{+}\hat{\beta}_{OLS}\) and ridge coefficients \(\hat{\beta}_{R}=\frac{1}{1+\lambda}\hat{\beta}_{OLS}\). It is obvious that the Ridge would keep all the predictors because the shrinkage factor \(\frac{1}{1+\lambda}>0\). But for the case of the Non-negative Garrote, the shrinkage factor could be zero if \(\lambda>\hat{\beta}_{OLS}\). It performs as the same as we elimates this predictor in our regression.
Why we should have the chance to have the shrinkage factor be zero? There is a example. John von Neumann famously said
With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.
By this he meant that one should not be impressed when a complex model fits a data set well. With enough parameters, you can fit any data set.
(In fact, someone truly draw this funny curve using 4-5 parameters… [6])
That’s why we need to select a subset of predictors. A mathmetical prove of the importance in reducing the number of predictors is provided on our lecture. For each additional predictor adds the same amount of variance \(\frac{\sigma^{2}}{N}\), regardless of whether its true coefficient is large or small.[4]
However, comparing the subset selection to the Non-negative Garrote, subset selection is discrete process, it is like making the shrinkage factor be 0 or 1. For the predictor you do not decide to drop, you leave it as before, but the Non-negative Garrote drop some and shrinken the others. It retains some predictors which have lower effect but shrink it smaller to reduce the variance of your model. It is a continuous process and hence is more stable.
2.3 the Lasso
Motivated by the idea of the Nonnegative Garrote, the new method Lasso came in 1995.
Revise with the two problems we talked at the beginning of this blog, the Ridge eases the problem 2, overfit with the existence of multicollinearity. Though the Nonnegative Garrote avoids some drawbacks of the Ridge, its solution depends on the sign and the magnitude of OLS estimates. In overfit or highly correlated setting where the OLS estimates behave poorly, the garotte may also suffer.[1]
This problem is obvious in the graph in the paper(Tibshirani, 1995) shows
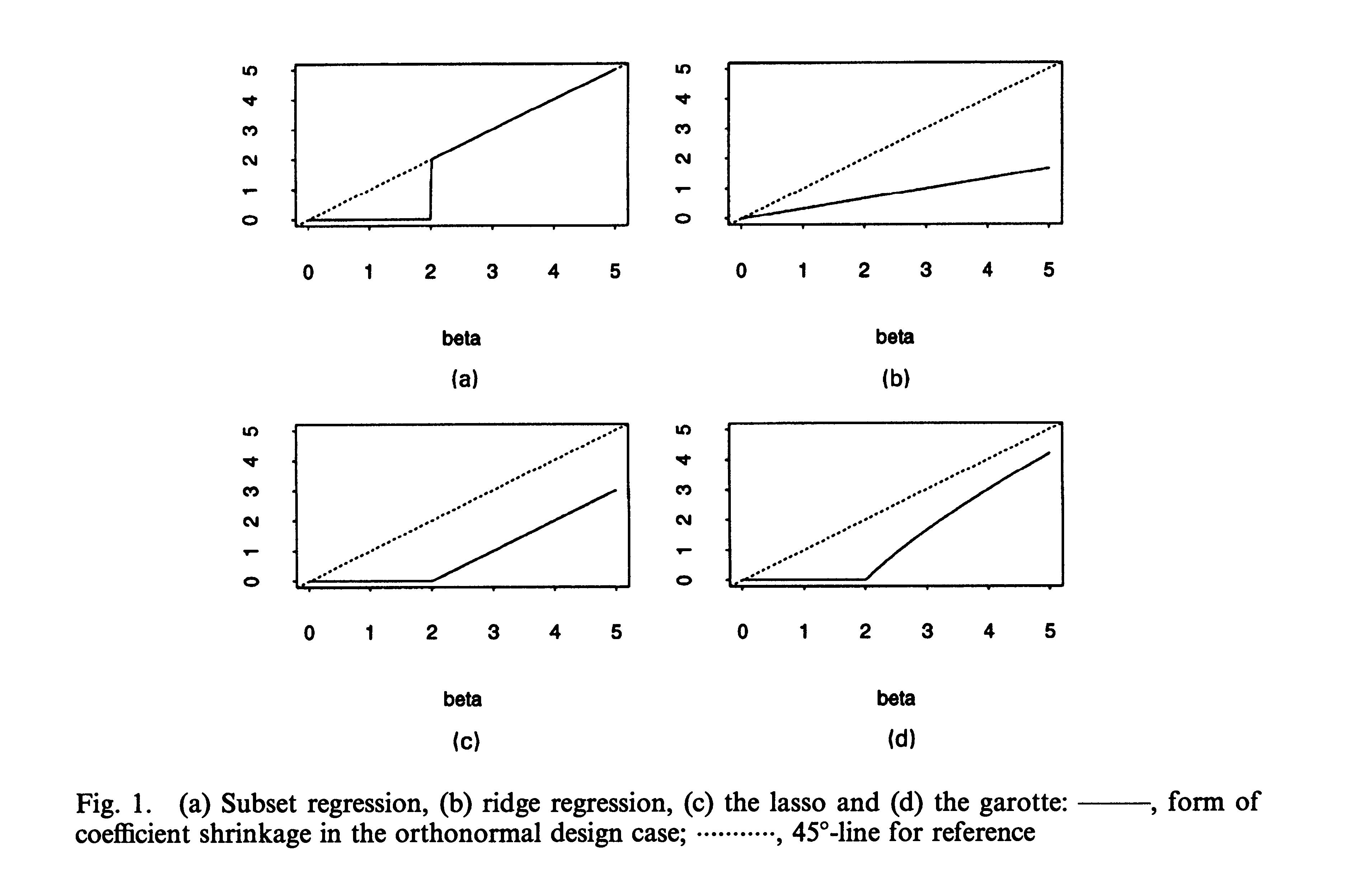
the garotte have the combination of advantages of subset regression and ridge regression. However, as the bata increase, the shinkage factor become bigger. But this problem does not exist in Lasso as the shrinkage effect is stable.
3.Conclusion
For all above, it sounds like the Lasso regression has lots of benefit comparing to the former methods. But we could not apply Lasso to all the situations. Remember the initial idea of regularization is to handle the problem with high demensions and overfit. More precisely, Lasso could be considered with an normal linear model with Laplace prior[7], it means we have the prior knowledge that our model has too many predictors and tends to be overfitted.
For example, in the paper, the author make a comparison between these methods in their relative merits.[1]
-
small number of large effects—-subset selection does best
-
small to moderate number of moderate-size effects—the lasso does best
-
large number of small effects—-the ridge regression does best
In conclusion, we should carefully determin that if we should do the regularization and choose the appropriate regularizers based on our prior belief.
references
[1] Tibshirani, Robert. “Regression Shrinkage and Selection via the Lasso.”[J]. Journal of the Royal Statistical Society. Series B (Methodological), vol. 58, no. 1, 1996, pp. 267–288. JSTOR, www.jstor.org/stable/2346178.
[2]Hoerl, Arthur E., and Robert W. Kennard. “Ridge Regression: Biased Estimation for Nonorthogonal Problems.” Technometrics, vol. 12, no. 1, 1970, pp. 55–67. JSTOR, www.jstor.org/stable/1267351.
[3]Michael A. Nielsen. “Neural Networks and Deep Learning”[M]. Determination Press. 2015
[4]Jiaming Mao. “Model_Selection_and_Regularization”[Z].2019-04-21.personal copy
[5]Breiman, Leo. “Better Subset Regression Using the Nonnegative Garrote.”[J]. Technometrics, vol. 37, no. 4, 1995, pp. 373–384. JSTOR, www.jstor.org/stable/1269730.
[6]J Mayer, K Khairy, J Howard. “Drawing an elephant with four complex parameters”[J]. American Journal of Physics 78, 648 (2010); https://doi.org/10.1119/1.3254017
[7]S. A. Dudani. The Distance-Weighted k-Nearest Neighbor Rule”[J]. IEEE Trans. on Systems, Man, and Cybernetics, Vol. SMC-6 (1976), pp. 325-327
[8]Jeffrey B. Arnold, “A Set of Bayesian Notes”[Z].https://jrnold.github.io/bayesian_notes/
Weekly Recommended Reading by myself
JOURNAL ARTICLE
The effect of welfare payments on work: Regression discontinuity evidence from Ecuador
Mariano Bosch and Norbert Schady
Journal of Development Economics, Volume 139, 2019, Pages 17-27, ISSN 0304-3878
DOI: 10.1016/j.jdeveco.2019.01.008.
Recently, I am learning several method evaluating the treatment effect. Here is a example using the fuzzy Regression discontinuity method. Different form the traditional sharp RD method, not all the sample in treatment group are being treated. In this case, it means that not all the eligible households receive payments. Therefore, they did a two stage regression, using the eligibility and other control variable to predict the true payment. And then regress the payment to the workchoice of womens.
Link
If you want to know more about how they can Drawing an elephant with four complex parameters, click to visit. https://aapt.scitation.org/doi/10.1119/
