- 1.Introduction
- 2.Syntax
- 3.Method Demonstration
- 4.Some notices using K-Nearest Neighbor classifier
- references
Nanjin Zeng(id:15220162202482) WISE IUEC 2016
You can also get a .lyn version in the same github folder because it is written with latex.
1.Introduction
In the lecture Classification, we have learnt a non-parametric method, K-nearest neighborclassifer. This method is founded by Cover and Hart (1967). As its founders stated, it may be the simplest nonparametric decision procedure[1], using the idea of “majority vote”. For the simplified version we learnt in class, it can be thought as[2]
\(\hat{p}(y=j|x)=\frac{1}{K}\sum_{i\in N_{K}(x)}I(y_{i}=j)\) with the desicion boundary of 0.5, where \(y\in\left\{ 1,\ldots,j\right\}\)
Though this method has some drawbacks, for example, the strong influence of a more frequent class, it is still a method being widely used in machine learning. In this blog, I would talk about how to perform KNN classification in Stata15 using the Credit Card Default data as same as our teacher demonstrated in R.
2.Syntax
discrim knn varlist [if] [in] [weight], group(groupvar) k(#) [options]
The groupvar is the variable of categories we want to classfied. Notice that it should be a numerical variable. If your categories are defined in string like the brand of ketchup, you should pre-treat them. For the k(#), it is the number of nearest neighbors you want to take in consideration. Large k reduced the noise on the classiifcation, but the boundaries would be less distinct. So, there is a trade-off setting the k. Some method could help you determin it wisely.[3]
The command performing KNN in stata is not some complex, but it contains some interesting options. In this part, I would introduce them and give a brief introduction to the idea behind them.
2.1 measure
For the measure of similarity or dissimilarity, we should compute the “distance” from the neighbour to the point being testing. Then we can choose the closest neighbors and make a “vote”. Stata gives us lots of measure in distance for us to choose.[4]
measure(L2) / measure(Euclidean)
This is the default one. It means that we use Euclidean distance.
\[E(x,y)=\sqrt{\sum_{i=0}^{n}\left(x_{i}-y_{i}\right)^{2}}\]measure(L1) / measure(manhattan)
The name comes from the distance taking taxi between blocks in manhattan. It means that we sum the absolute-value distance in each dimension.
\[E(x,y)=\sum_{i=0}^{n}|x_{i}-y_{i}|\]Many other measures could be used, based on the actual need, including Minkowski distance, Canberra distance and so on. Noticed that if you choose a continuous measure, you should normalize your data. That would make different variable unit-free and comparable.
2.2 priors
In a bayesian’s view, if we know the prior probabilities in each categories, we should take it into consideration. This term allow us to specify the prior probabilities. Moreover, it could ease the problem of majority vote making the frequent class dominate the prediction.
priors(proportional)
It means that we do not make any adjustement. The prediction is simply based on observed data.
priors(equal)
This is the default one. It means that we specify a non-informative prior and assume an equal probability in each group.
priors(matname)
You can use a matrix to specify the prior probalities for each categories.
2.3 ties
Ties refer to the multiple equal outcomes[5] when we doing prediction using the trainning data. For example, when \(k=2\) if the nearest 2 point belongs to different groups, we cannot determin the prediction for this point using the rule of majority-vote. Though we can reduce the oucurrence by some method, like the simplest “k should be odd number”, it would bother us we we do KNN in a high dimension. In the annotation(17) on the slides, ties are broken at random. It means these points would be randomly assigned to each category. (in stata, “ties(random)”)Also we could define how to treat them in stata.
ties(missing)
This is the default one. It means we do not make any predictions in these point.
ties(first)
It means that ties are set to the first tied group.
ties(nearest)
It means that the predition in ties would base on the nearest point. But it may still remain in a tie in some extreme situations. Then we do not make any predictions in these point.
3.Method Demonstration
To show it intuitively, I use the same data (Credit Card Default data) in Stata15. In this example, as we did in the lecture using R, we perform the KNN on the trainning data and see the effect \(\left(E_{in}\right)\).
import delimited “C:\Users\91367\Desktop\junior 2nd term\microeconometrics\hw\knn\Default.csv”
generate default_num=0 if default==”No”
replace default_num=1 if default==”Yes”
To be recognize as a group variable, since categories are defined in string “No” and “Yes”, we should give them a number as an indicator.
egen ba_std=std(balance)
egen in_std=std(income)
We normalize the variable to have a zero mean and 1 stand error. That is a necessary step using KNN, otherwise you put unequal weight in the variables and the distances are unreliable.
discrim knn ba_std in_std, group(default_num) k(5) priors(proportional) ties(random)
The result using KNN
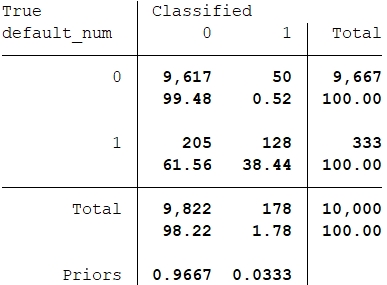
From this table, it reveals that the error is not so small. We make 205 false-negative prediction and 50 false-positive predictions on the trainning data. In this case, false-negative result is critical because it means that we give credit to someone who finally defaulted. However, this result is on the trainning data. We should combine this idea with other method like cross-validation to evaluate the validity of our classifier.
4.Some notices using K-Nearest Neighbor classifier
From the example, we can feel some drawbacks in our “simple” K-nearest Neighbor classifier we need to notice.
- When the program runs into the final part of KNN, it takes a long time until it gives out the result. That is something being talked in almost every materials about KNN. As a “lazy method”, it retain the trainning data and search through the data for the k nearest observations each time a classificatuion or prediction is performed.[6] However, you could ingore the trainning data after you build the classifier performing linear discriminant analysis or logistic discriminant analysis. So, if you have a large number of sample, you should consider if it is proper to use K-Nearest Neighbor Classifier.
- As I mention serveal times above, the KNN suffered from the drawback of majority vote. One measure is to put the prior probabilities into consideration. (using prior(matname)) But a simple one is to change our method to “weighted k-nearest neighbor classifier”[7] A common way to weight is to giving each neighbor a weight of \(\frac{1}{d}\), where \(d\) is the distance to the neighbor. It reduces the influence from a further point, but not so much comparing to setting k=1. That may work well when the difference in the number of each categories is large. It prevents the result being dominated by a more frequent group.
- Though K-Nearest neighbor is a non-parametric method, it still have assumption. The basic idea is the result should be locally homogeneous. Using a intuitive example talking by many others “Your grandparents are republicants. Your parents are republicants. Your neighbour are all repubilicants. But you can still be a democrats!” You should check your economic idea if it is reasonable to imply this “lazy method”.
references
[1] T. M. Cover, P. E. Hart. “Nearest Neighbor Pattern Classification”[J]. IEEE Trans. on Information Theory, Vol. 13, No. 1. (January 1967), pp. 21-27
[2]Jiaming Mao. “Classification”[Z].2019-04-10.personal copy
[3]Everitt, B. S., Landau, S., Leese, M. and Stahl, D.. “Miscellaneous Clustering Methods, in Cluster Analysis”[M[.John Wiley & Sons, Ltd, Chichester, UK. 2011
[4]Stata Statistics/Data Analysis. “measure_option”[Z]. 2019-04-11.
[5]Joseph M.Hilbe. “Logistic Regression Models”[M].Chapman and Hall/CRC. 2009
[6]Stata Statistics/Data Analysis. “discrim knn”[Z]. 2019-04-11.
[7]S. A. Dudani. The Distance-Weighted k-Nearest Neighbor Rule”[J]. IEEE Trans. on Systems, Man, and Cybernetics, Vol. SMC-6 (1976), pp. 325-327
[8]Charles D Mallah, James Orwell. “Probabilistic Classication from a K-Nearest-Neighbour Classier”.Computational Research 1(1): 1-9, 2013
Weekly Recommended Reading by myself
The policy of eliminating tolls during holidays generates a significant loss of social welfare.
JOURNAL ARTICLE
Highway toll and air pollution: Evidence from Chinese cities
Shihe Fu, Yizhen Gu
Journal of Environmental Economics and Management Volume 83, May 2017, Pages 32-49
DOI: 10.1016/j.jeem.2016.11.007
This policy is well known and supported by a large number citizens. However, whether this policy is economical enough to imply is still being discussed. For example, most of us has experienced that the congestion in highway is unavoidable in national holiday. This paper give us an reasonable estimation on the welfare loss due to the policy. Moreover, it analyzes that the drivers do not shifted their trips from before and after “no toll” periods to the “no toll” period. That makes the result more reliable.
