Nanjin Zeng(id:15220162202482) WISE IUEC 2016
Bug fixed! You need not wait for mathemetical formulas to load.
You can also get a .lyn version in the same github folder because it is written with latex.
1.Introduction
In the lecture, we have learnt the learning problem for noiseless target and for noisy target, besides the Approximation-Generalization Tradeoff. The central part of this tradeoff is to find an “appropriate” hypothesis set. It means that we should choose a hypothesis set with proper complexity, then the bias and the variance are both considered to be low.
(For this part, I highly recommend to read the material in “Notes and Resources” named “learning without noise[1]” and “learning with noise[2]”, it uses a constructed data set and the degree of polynomial to illustrate the benefit and the harm using a complex model in different situations. These two articles are also mentioned by our professor in class.)
And to describe the complexity, we were introduced to two new concepts:
The growth function for a hypothesis set His defined by[3]
\[m_{H}\left(N\right)=\max_{x_{1},\cdots,x_{N}\epsilon X}\mid H\left(x_{1},\cdots,x_{N}\right)\mid\]
i.e.\(m_{H}\left(N\right)\) is the maximum possible number of dichotomies Hcan generate on a data set of N points.
The Vapnik-Chervonenkis (VC) dimension of H, denoted \(d_{vc}\left(H\right)\), is the size of the largest data set that H can shatter.
These concept sounds a little bit incomprehensible to us undergraduate students. In addition, the professor does not mention too much in this part but concentrate on the generally understanding the meaning to balance the bias and variance of the model. So, for this blog, I want to introduce these two concepts precisely and intuitively. (For mathematical proof, you can read the article which I mention below.)
2.Back to the origin
I find the literature of Vapnik and Chervonenkis, on the uniform convergence of relative frequencies of events to their probabilities (translated ver. in English), theory of probability and applications, volume 12, 1971. I consider that it is the origin of these two concepts. Though in this article, they did not use the term of “VC dimension”, I find a property of grow function could be useful for us.
Property of the growth function
The growth function for a class of events S has the following property : it is either identically equal to \(2^{r}\) or is majorized by the power function \(r^{n}+1\), where n is a constant equaling the value of r for which the equality \(m^{S}(r)=2^{r}\) is violated for the first time.[4]
The parameter n is what we call VC dimension these days! To many kinds of H, we cannot find a general solution for us to determin VC dimension, but in some simple situation, this relationship could help us understanding the meaning of growth function and VC dimensions.
3.Example
With the example in appendix I in our lecture, we could test this property and relate it with VC dimension.
3.1 Positive Rays
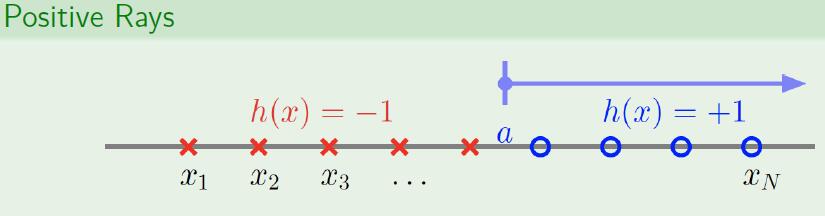
Let us condider a simple situation.
If there is only 1 point, for the division point lies on left or right, we have 2 dichotomies. \(m_{H}(1)=2\), which satisfies \(m_{H}(1)=2^{1}\)
If there is 2 point, there is only 3 dichotomies. \(m_{H}(2)=3\), which violates \(m^{S}(r)=2^{r}\) and turn to \(m^{S}(2)=2^{1}+1\) . The positive ray could not divide them into “+,-“.
If there is more than 3 point, \(m^{S}(r)=r^{1}+1=r+1\), as it stated in the appendix of our lecture notes.
So, for this case, \(d_{vc}\left(H\right)=n=1\)
3.2 Set of Lines (liner separators)
In \(\mathbb{\mathbb{R}}^{2}\), for less than 3 points, we have proved in class that it could solve any situations. \(m^{S}(r)=2^{r}\)for \(r\leq3\)
As we mentioned in the lecture, when it comes to 4 points, there are two situation we cannot divide them using any line.
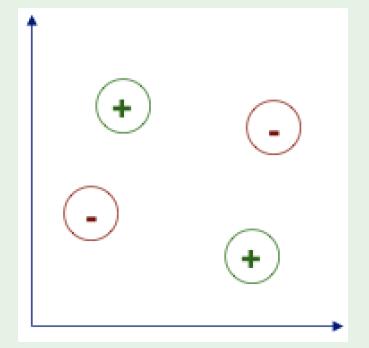
So, for this case, \(m^{S}(4)=4^{3}+1=65\), \(d_{vc}\left(H\right)=n=3\).
3.3 Convex Sets
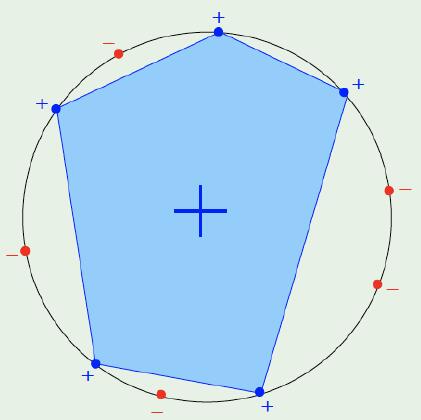
Obviously, \(m^{S}(r)=2^{r}\). All we have to do is to connect the neighbour point which is “+”. The is no finite n could violate the equity.
For this case, \(d_{vc}\left(H\right)=\infty\)
4.conclusion
For which I mentioned above, I want to emphasize that the VC dimension is is a constant equaling the value of r for which the equality of growth function \(m^{S}(r)=2^{r}\) is violated for the first time.
After last Tuesday’s class, my classmate asked me what is the VC dimension. But I don’t truly understand this concept either. I hope that could be useful for us learning these concepts.
references
[1] Rahul Dave.Learning a model[OL].2019-03-11.http://am207.info/wiki/noiseless_learning.html
[2]Rahul Dave.Noisy Learning[OL].2019-03-11.http://am207.info/wiki/noisylearning.html
[3]Jiaming Mao.Foundations_of_Statistical_Learning[Z].2019-03-11.https://github.com/jiamingmao/data-analysis/blob/master/Lectures/Foundations_of_Statistical_Learning.pdf
[4]Vapnik, V. N.; Chervonenkis, A. Ya. (1971). “On the Uniform Convergence of Relative Frequencies of Events to Their Probabilities”[J]. Theory of Probability & Its Applications. 16 (2): 264. doi:10.1137/1116025
Weekly Recommended Reading by myself
Since all models are wrong the scientist must be alert to what is importantly wrong. It is inappropriate to be concerned about mice when there are tigers abroad.
JOURNAL ARTICLE
Science and Statistics
George E. P. Box
Journal of the American Statistical Association Vol. 71, No. 356 (Dec., 1976), pp. 791-799 Published by: Taylor & Francis, Ltd. on behalf of the American Statistical Association
DOI: 10.2307/2286841
I find this article when I want to learn more about George E. P. Box, who states the famous “All models are wrong but some are useful”. In this article, he drew some story of R.A. Fisher, to introduce how to use statistic in rearch of other scientific field. And he gave a early concept of data analysis and data getting in the process of scientific investigation. You can read it as a pastime because most of the article is vivid narration and a little bit math. I think it’s highly related with much concepts we learnt at the course mathematical statistics. And you can know how a early statistician work at that time.
